Gini-Koeffizient

Definition

Der Gini-Koeffizient (oder Gini-Index) gibt den Grad der Ungleichheit der Einkommensverteilung, z.B. in einem Land oder einer Region, nach dem häuslichen Pro-Kopf-Einkommen (1) an. Die Berechnung des Gini-Koeffizienten geht aus der so genannten Lorenz-Kurve hervor. Die Lorenz-Kurve besteht aus verschiedenen Punkten, die die Relation zwischen dem kumulativen Prozentsatz der Bevölkerung (x-Achse) und dem kumulativen Prozentsatz des Einkommens dieser Bevölkerung (y-Achse) wiedergeben. Mit anderen Worten: Aus der Lorenz-Kurve lässt sich ablesen, wie das Gesamteinkommen einer Volkswirtschaft auf einen bestimmten Anteil der Bevölkerung entfallen (z.B. 90% des Einkommens fallen auf 10% der Bevölkerung etc.).

Lorenz-Kurve

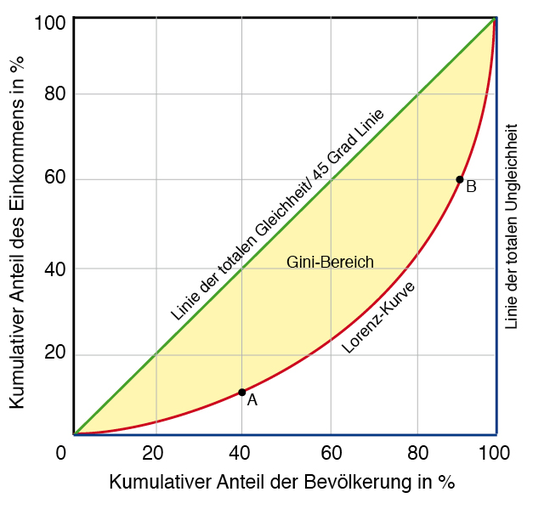
(vgl.: Temkin, L.S. (1996) Inequality. Oxford: Oxford University Press, S. 129)

Im folgenden Beispiel (siehe Graphik) einer hypothetischen Lorenz-Kurve (rot) steht z.B. Punkt A für die Aussage „die unteren 40% der Bevölkerung besitzen 10% des gesamten Einkommens“, und Punkt B für die Aussage „die unteren 90% der Bevölkerung besitzen 60% des gesamten Einkommens“.

Die Lorenz-Kurve befindet sich immer zwischen zwei Linien, der „Linie der totalen Gleichheit“ und der „Linie der totalen Ungleichheit“. Dabei steht die „Linie der totalen Gleichheit“, d.h. die „45 Grad Linie“ (hier grün), für eine gleiche Einkommensverteilung. Entlang dieser Linie ist das Einkommen aller Individuen identisch, da an jedem Punkt auf der Linie gleichermaßen gilt: x% des Einkommens werden von x% der Bevölkerung verdient (z.B. 50% des Einkommens entfallen auf genau 50% der Bevölkerung, 60% der Einkommens entfallen auf 60% der Bevölkerung usw.).

Die „Linie der totalen Ungleichheit“ (hier blau) wiederum gibt die genau entgegengesetzte Situation wieder, nämlich dass nur einem einzigen Individuum das gesamte Einkommen der Gesellschaft zukommt.

Für unsere Analyse ist nun der Abstand zwischen der Lorenzkurve und der „45 Grad Linie“ interessant, also um wie viel die beobachtete Einkommensverteilung von der Gleichverteilung abweicht. Hierzu berechnet man den Prozentsatz des Anteils der Fläche zwischen der „45 Grad Linie“ und der Lorenzkurve an der Gesamtfläche. Das Ergebnis dieser Berechnung wird entweder als Gini-Koeffizient dargestellt (einem Wert zwischen 0 und 1) oder als Gini-Index (indem man den Gini-Koeffizienten mit 100 multipliziert.).

Dabei bedeutet der Wert 0, dass es totale Gleichheit in der Einkommensverteilung gibt (die Lorenzkurve entspricht in diesem Fall der „45 Grad Linie“, die Fläche zwischen den Linien ist somit Null); der Wert 1 (Gini-Koeffizient) oder 100 (Gini-Index) bringt wiederum zum Ausdruck, dass nur einem Individuum das gesamte Einkommen der Volkswirtschaft zukommt und dass das Einkommen der anderen somit Null ist (die Lorenzkurve entspricht in diesem Fall der „Linie der totalen Ungleichheit“, die Fläche zwischen der „45 Grad Linie“ und der Lorenzkurve beträgt 1). D.h., je näher der Wert an 0 ist, desto gleicher ist die Verteilung des Einkommens. Im Allgemeinen werden Länder mit einem Gini-Koeffizienten zwischen 0,50 und 0,70 (Gini-Index zwischen 50 und 70) als sehr einkommensungleich, und die mit einem Gini-Koeffizienten zwischen 0,20 und 0,35 (Gini-Index zwischen 20 und 35) als relativ einkommensgleich bezeichnet (Willis 2005: 9)¹.

Beispiel: Brasilien

Brasilien ist in Bezug auf den Gini-Koeffizient ein gutes Beispiel, da es weltweit als eines der Länder mit der größten Ungleichheit in der Einkommensverteilung gilt und außerdem eines der wenigen Länder ist, die den Gini Index bis auf die Munizipienebene herunter berechnen (s. IPEADATA, statistische Datenbank der öffentlichen, föderativen Stiftung Instituto de Pesquisa Econômica Aplicada - IPEA). Dieses verhilft zu einer besseren Veranschaulichung der Einkommensverteilung und lässt unter anderem Aussagen über die regionalen Unterschiede innerhalb Brasiliens sowie deren mögliche Ursachen zu.

Der aktuellste Gini-Koeffizient Brasiliens (2008) liegt, laut IPEADATA, bei 0,548. Die Einkommensverteilung innerhalb Brasiliens ist somit im Vergleich zu anderen Schwellenländern wie zum Beispiel China sehr ungleich (s. Tabelle 1). Seit 1998 ist der Gini-Koeffizient Brasiliens von 0,600 relativ konstant gesunken (s. Tabelle), was durchaus den Schluss zulässt, dass eine aktive Sozial- und Entwicklungspolitik (wie unter den Regierungen Cardosos und Lulas) den Gini-Koeffizient positiv beeinflussen kann.