Berechnungsmethoden
Berechnung der Inflationsraten für verschiedene Zeitintervalle
Die Statistikämter veröffentlichen oft eine Vielzahl von verschiedenen Inflationsraten wie z.B. die monatliche Inflationsrate, die jährliche Inflationsrate und die durchschnittliche jährliche Inflationsrate. Darüber hinaus ist es möglich tägliche Inflationsraten zu ermitteln.
Von der jährlichen Inflationsrate wird gesprochen, wenn die Entwicklung des Verbraucherpreisindizes z.B. zwischen dem Januar 2010 und dem Januar 2011 betrachtet wird. Sie wird über die Methode von Laspeyres anhand der folgenden Formel berechnet:
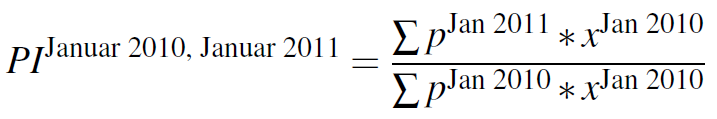
mit PI, dem Wert des Preisindizes, p den Preisen und x für ein Gut im Warenkorb. Dahingegen handelt es sich bei der durchschnittlichen jährlichen Inflationsrate um den Durchschnitt der jährlichen Inflationsraten, welcher sich nach der Formel
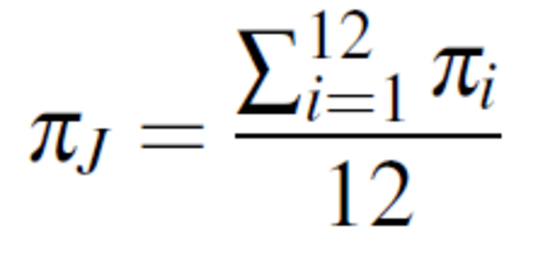
berechnet. Hierbei steht πJ für die durchschnittliche jährliche Inflationsrate und π für die jährliche Inflationsrate gemessen im Monat i.
Zur Ermittlung der monatlichen Inflationsrate stehen zwei Berechnungsmöglichkeiten zur Verfügung. Zunächst lässt sich die Inflationsrate über den Laspeyres-Index berechnen, hierzu wird der Preis eines definierten Warenkorbes in einem bestimmten Monat in Relation zum Preis des gleichen Warenkorbes im Vormonat gesetzt. Diese Methode wird z.B. vom Statistischen Bundesamt und dem Bureau of Labor Statistics in den USA verwendet.
Wenn einem jedoch nur jährliche Inflationsraten zur Verfügung stehen, man aber die monatliche Inflationsrate wissen möchte, dann lässt sich die monatliche Inflationsrate über den geometrischen Mittelwert aus der jährlichen Inflationsrate ermitteln. Der geometrische Mittelwert errechnet sich anhand der Formel:
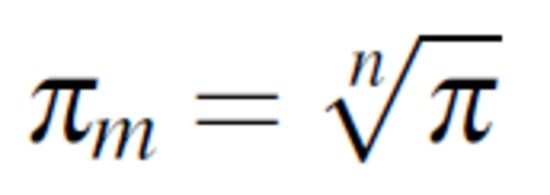 .
.
Hierbei steht πm für die monatliche Inflationsrate, π für die jährliche Inflationsrate und n=12 für die Anzahl der Monate eines Jahres. Für eine jährliche Teuerungsrate von 15% ergibt sich anhand der oben genannten Formel
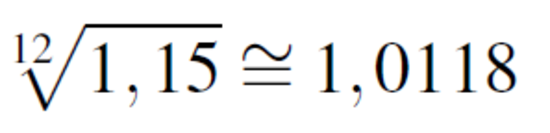
eine monatliche Inflationsrate von näherungsweisen 1,18%.
Die tägliche Inflationsrate lässt sich nach derselben Methode berechnen (in diesem Fall steht πt für die tägliche Inflationsrate, π für die jährliche Inflationsrate und n=360 für die Tage des Jahres, in der Finanzmathematik rechnet man zumeist mit einem Jahr gleich 360 Tagen und einem Monat gleich 30 Tage)
![]()
Die Berechnung täglicher Inflationsraten ist jedoch nur bei sehr hohen monatlichen oder jährlichen Inflationsraten von Interesse. Beispielsweise würde eine vergleichsweise hohe jährliche Inflation von 15% aus dem vorangegangen Beispiel eine tägliche Inflationsrate von 0,038% bedeuten. Wenn man hingegen eine jährliche Inflationsrate von 20.000% wie in Bolivien zwischen August 1984 und August 1985 in Betracht zieht, so ergibt sich
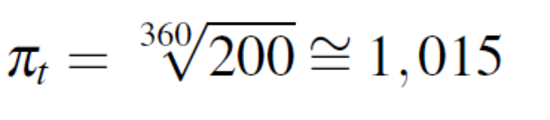
und somit eine tägliche Inflationsrate von 1,5%.
Allerdings ist Vorsicht angesagt: Bei den anhand des geometrischen Mittelwertes ermittelten Inflationsraten handelt es sich lediglich um eine durchschnittliche Inflationsrate. Es ist also nicht zulässig auf Grund dieser Rechnung die Aussage zu treffen, dass die Inflation im Dezember 2009 πm Prozent betragen habe. Um eine sinnvolle Aussage zur Inflation in einem bestimmten Monat treffen zu können, muss die Inflationsrate nach Laspeyres-Index herangezogen werden. Anhand der untenstehenden Grafik lässt sich erkennen, dass die Entwicklung des Verbraucherpreisindex nicht gleichmäßig verläuft sondern Schwankungen unterworfen ist.
Entwicklung des Konsumentenpreisindex (USA, 2005-2007)
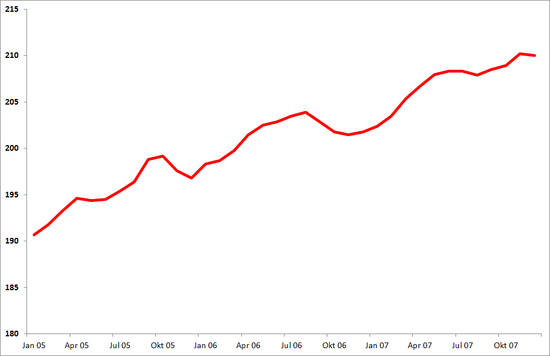
Quelle: Federal Reserve Bank of St. Louis FRED
Zinsrechnung
Für ökonomische Fragestellungen, insbesondere im Bereich der Mikrofinanzen, ist es oft interessant, die Zinszahlungen eines Kredites bzw. die Zinserlöse einer Einlage zu berechnen. Im Folgenden wollen wir die Formel zur Berechnung der Zinsen herleiten. Bei einem jährlichen Zinssatz von 10% verzinst sich eine Einlage von 100€ mit 10€ pro Jahr. Dies lässt sich wie folgt berechnen
![]()
Für ökonomische Fragestellungen, insbesondere im Bereich der Mikrofinanzen, ist es oft interessant, die Zinszahlungen eines Kredites bzw. die Zinserlöse einer Einlage zu berechnen. Im Folgenden wollen wir die Formel zur Berechnung der Zinsen herleiten. Bei einem jährlichen Zinssatz von 10% verzinst sich eine Einlage von 100€ mit 10€ pro Jahr. Dies lässt sich wie folgt berechnen
![]()
Mit dem Endwert E für die Summe aus Zinsen und Einlage zum Ende der Laufzeit von einem Jahr bei einer Verzinsung von 10%. Es ist einfach zu erkennen, dass anhand der beiden oben genannten Formeln eine Vielzahl von Berechnungen möglich ist. So können z.B. die nach vier Monaten angefallenen Zinsen anhand von
![]()
berechnet werden. Mit m für die Anzahl der Monate, welche der Kredit läuft oder die Einlage verzinst wird. Der Zusammenhang mit der Formel für die jährliche Verzinsung ergibt sich, wenn man für m zwölf Monate einsetzt (12:12=1). Analog lässt sich die Formel auch für die täglich anfallenden Zinsen aufstellen. So kann die täglich anfallende Zinszahlung anhand von
![]()
mit t der Anzahl der Tage berechnet werden. Auch hier gilt analog zum Beispiel mit den monatlichen Zinszahlungen zeigen, dass für 360 Tage (360:360=1) die Grundformel gilt.
Es zeigt sich, dass sich anhand der oben genannten Formel nicht nur der Endbetrag und der Zins berechnen lassen, sondern durch Umstellen der Formel bei gegebenen Werten auch das Anfangskapital K
![]()
den Zinssatz i
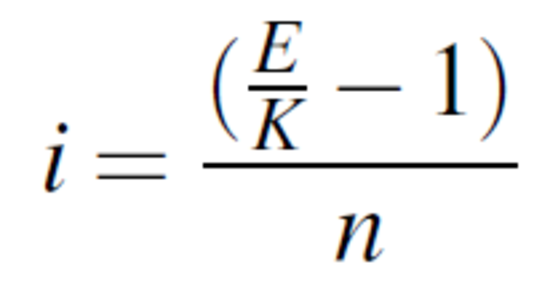
und die Laufzeit n
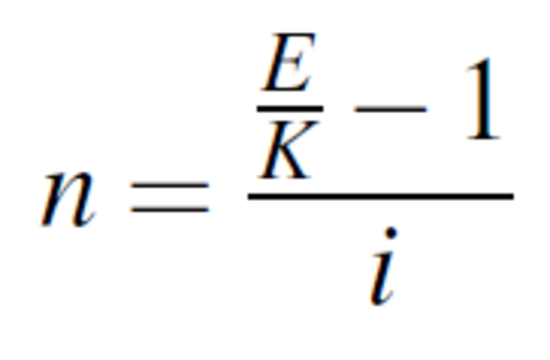
berechnet werden können.
Die hier vorgestellte Zinsformel ist in ihrer Form allerdings statisch, sie berücksichtigt nicht den sogenannten Zinseszins. Dies soll am folgenden Beispiel verdeutlicht werden. Ein Bankberater berechnet für eine Einlage in Höhe von 100€ zu einem Zinssatz von 10% mit einer Laufzeit von 2 Jahren nach folgender Formel
![]()
einen Endwert von 120€. Überlegen wir uns nun folgendes: wir legen den Betrag von 100€ zu 10% für ein Jahr an. Wie bereits berechnet bekommen wir nach einem Jahr 110€ ausgezahlt. Wenn wir diese erneut für ein Jahr zu einem Zinssatz von 10% anlegen, erhalten wir nach insgesamt 2 Jahren einen Endwert von 121€. Dies lässt sich auch schnell anhand der Formel
![]()
berechnen. Hier steh E für den Endwert, K für das Anfangskapital, i für den Zinssatz und n für die Dauer der Verzinsung in Jahren. Zur Berechnung der Verzinsung auf Monatsbasis rufen wir uns kurz vor Augen, dass sich der Ausdruck n für ein Jahr auch in Tagen ausdrücken lässt: 360:360=1. Die Einlage von 100€ wächst nach einem Tag, hierbei steht t für die Anzahl der Tage, welche das Kapital angelegt wird, auf
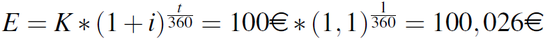
an. Zur Berechnung der monatlichen Verzinsung der Einlage kann man auf die Tatsache zurückgreifen, dass sich der Exponent n auch als Bruch (12:12=1) darstellen lässt. So erzielt unsere Einlage nach vier Monaten
![]()
Auch die oben genannte Formel lässt sich bei gegebenen Werten einfach umstellen. So kann das Startkapital K
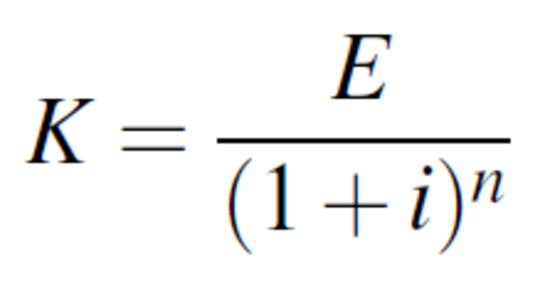
der Zinssatz i
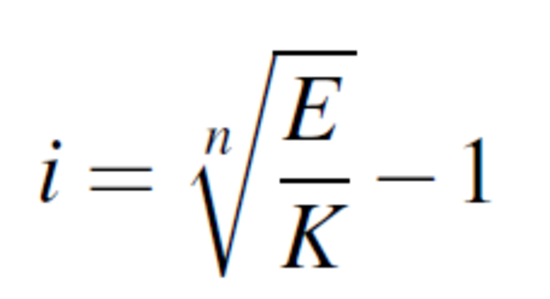
und die Laufzeit n
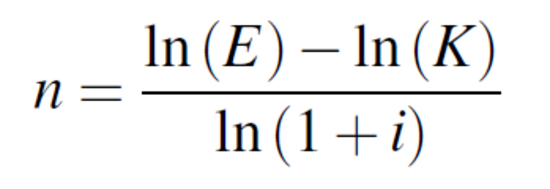
berechnet werden (ln steht hier für den Logarithmus naturalis).
Der Realzins
Für ökonomische Anwendungen, insbesondere in den Mikrofinanzen, ist der nominale Zinssatz oft nicht von Bedeutung, vielmehr interessieren sich Anleger und Anlegerinnen, sowie Kreditnehmer und Kreditnehmerinnen für den realen Zinssatz. Dies lässt sich darauf zurückführen, dass z.B. eine Anlegerin nicht primär daran interessiert ist wie viele Geldeinheiten sie aus ihrer Investition zieht, sondern welche Konsummöglichkeiten ihr in der Zukunft zur Verfügung stehen. Da die Konsummöglichkeiten aus der Spareinlage durch Teuerungen (also durch Inflation) beschnitten werden können, hat die Investorin das Interesse den inflationsbereinigten Zinssatz oder realen Zinssatz zu erfahren. Anhand einer logarithmischen Approximation kann gezeigt werden, dass der Realzins näherungsweise
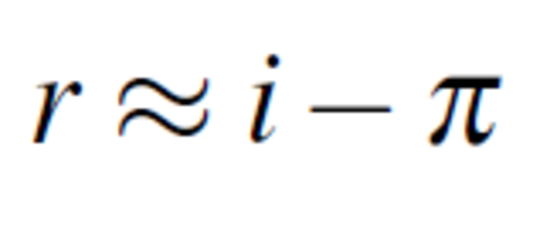
beträgt (hierbei steht r für den Realzins, i für den Nominalzins und π für die Inflationsrate). Bei einer Inflationsrate von 3% und einem Nominalzins von 4% wird eine Anlage real mit etwa 1% verzinst.